Densidades
En la estadística se trabaja con una alta gama de distribuciones discretas y continuas. En la mayoría de casos se usan las distribuciones continuas, como la distruibución normal, log-normal, t-student, \(\chi^2\), entre otras.
Función de densidad de una distribución Normal
Ahora se realizará un ejemplo de cómo graficar la función de densidad de la distribución normal, la cual tiene por fórmula:
\[ f(x)=\frac{1}{\sqrt{2\pi\sigma}}e^{\frac{-(x-\mu)^2}{2\sigma^2}},\] donde \(-\infty< x < +\infty\) es una variable cuantitativa.
Como encontrar y realizar gráficas de densidad para esta variable es muy engorroso manualmente, utilizaremos el programa R que brinda el comando predeterminado dnorm(x,mu,sigma), el cual encuentra la función de densidad de la variable \(x\) bajo el \(\mu\) y el \(\sigma\) especificados por el investigador.
Es importante aclarar que R también posee otros comandos predeterminados para la distribución normal, tales como pnorm,rnorm y qnorm.
Ahora se iniciará generando una muestra de tamaño 200 de una población normal de media 10 y desviación típica 1.
x<-rnorm(200, mean= 10, sd=1)
xDe esta muestra se puede obtener una descripción básica como la media muestral y la desviación estandar de \(x\).
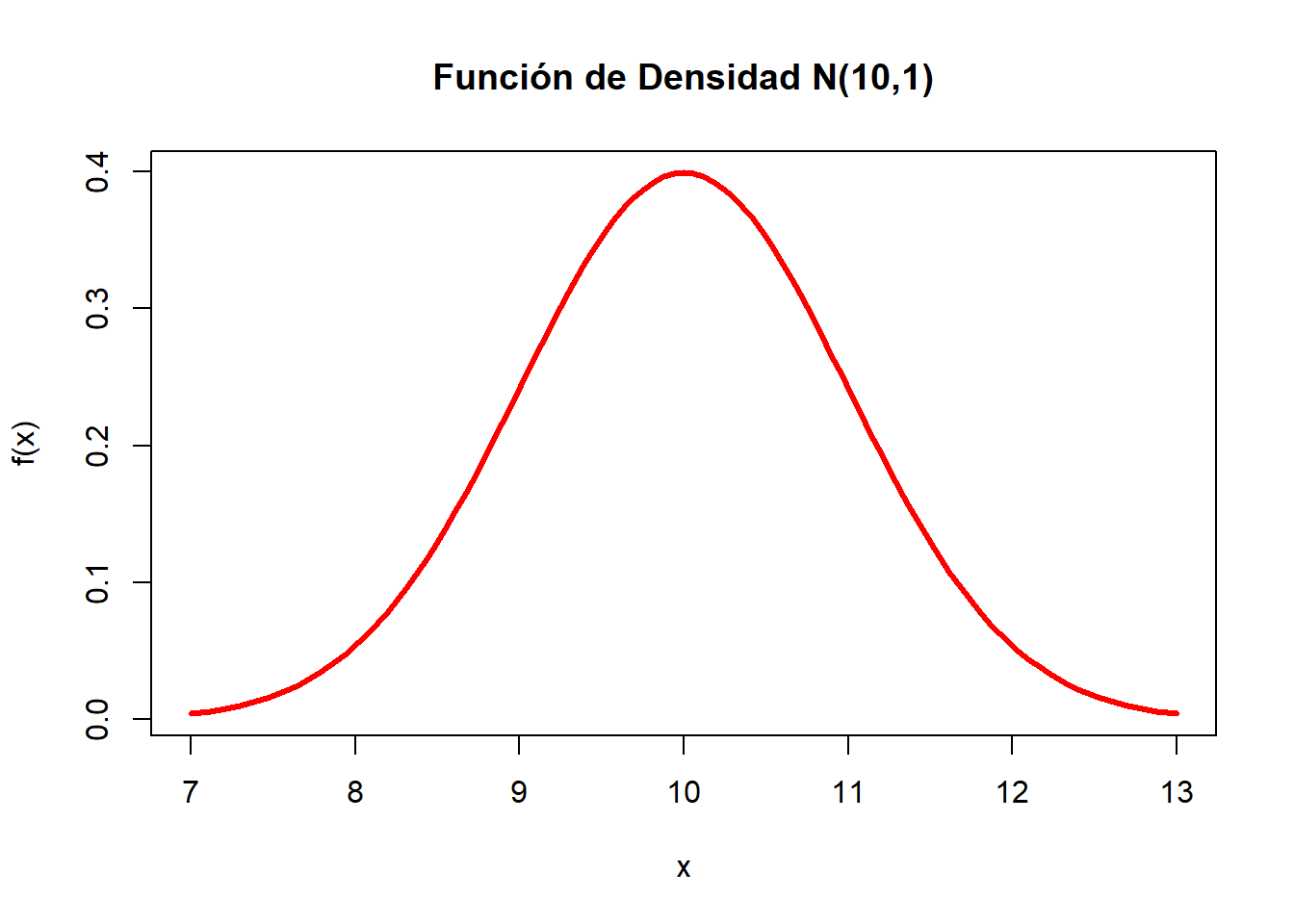
Ahora, con la información que se tiene, se generará el gráfico de densidad correspondiente:
curve(dnorm(x,10,1), from = 7, to = 13, col="red",lwd=3,
xlab="x",ylab="f(x)",main="Función de Densidad N(10,1)")